Table of Contents

• Lipschitz Monotonic Networks
• Installation
• Requirements
• Usage
• Examples
  • Monotonicity
  • Robustness
  • Lipschitz NNs can describe arbitrarily complex boundaries

Lipschitz Monotonic Networks

Implementation of Lipschitz Monotonic Networks, from the ICLR 2023 Submission: https://openreview.net/pdf?id=w2P7fMy_RH and the repo is on github.

The code here allows one to apply various weight constraints on torch.nn.Linear layers through the kind keyword. Here are the available weight norms:

"one",      # |W|_1 constraint
"inf",      # |W|_inf constraint
"one-inf",  # |W|_1,inf constraint
"two-inf",  # |W|_2,inf constraint

Installation

pip	conda
pip install monotonicnetworks	conda install -c conda-forge monotonicnetworks

Note that the package used to be called monotonenorm and was renamed to monotonicnetworks on 2023-07-15. The old package is still available on PyPI and conda-forge, but will not be updated.

(deprecated) pip install monotonenorm

(deprecated) conda install -c okitouni monotonenorm

Requirements

Make sure you have the following packages installed:

• torch (required)
• matplotlib (optional, for plotting examples)
• tqdm (optional, to run the examples with a progress bar)

Usage

Here’s an example showing two ways to create a Lipschitz-constrained linear layer.

from torch import nn
import monotonicnetworks as lmn

linear_by_norming = lmn.direct_norm(nn.Linear(10, 10), kind="one-inf") # |W|_1,inf constraint
linear_native = lmn.LipschitzLinear(10, 10, kind="one-inf") # |W|_1,inf constraint

The function lmn.direct_norm can apply various weight constraints on torch.nn.Linear layers through the kind keyword and return a Lipschitz-constrained linear layer. Alternatively, the code in montonenorm/LipschitzMonotonicNetwork.py contains several classes that can be used to create Lipschitz and Monotonic Layers directly.

• The LipschitzLinear class is a linear layer with a Lipschitz constraint on its weights.

• The MonotonicLayer class is a linear layer with a Lipschitz constraint on its weights and monotonicity constraints that can be specified for each input dimension, or for each input-output pair. For instance, suppose we want to model a 2 input x 3 output linear layer where the first output is monotonically increasing in the first input ([1, 0]), the second output is monotonically decreasing in the second input ([0, -1]), and the third output is monotonically increasing in the first input and monotonically decreasing in the second input ([1, -1]). We can do this by specifying the monotonicity constraints as follows:

import monotonicnetworks as lmn

linear = lmn.MonotonicLayer(2, 3, monotonic_constraints=[[1, 0], [0, 1], [1, -1]])

Using a 1D tensor for the constraint assumes that they are the same for each output dimension. By default, the code assumes all outputs are monotonically increasing with all inputs.

• The MonotonicWrapper class is a wrapper around a module with a Lipschitz constant. It adds a term to the output of the module which enforces monotonicity constraints given by monotonic_constraints. The class returns a module that is monotonic and Lipschitz with constant lipschitz_const. This is the preferred way to create a monotonic network. Example:

from torch import nn
import monotonicnetworks as lmn

lip_nn = nn.Sequential(
    lmn.LipschitzLinear(2, 32, kind="one-inf"),
    lmn.GroupSort(2),
    lmn.LipschitzLinear(32, 2, kind="inf"),
)
monotonic_nn = lmn.MonotonicWrapper(lip_nn, monotonic_constraints=[1,0]) # first input increasing, no monotonicity constraints on second input

Note that one can stack monotonic modules.

• The SigmaNet class is a deprecated class that is equivalent to the MonotonicWrapper class.

• The RMSNorm class is a class that implements the RMSNorm normalization layer. It can help when training a model with many Lipschitz-constrained layers.

Examples

Check out the Examples directory for more details. Specifically, Examples/flower.py shows how to train a Lipschitz Monotonic Network to regress on a complex decision boundary in 2D (under Lipschitz NNs can describe arbitrarily complex boundaries), and Examples/Examples_paper.ipynb for the code used to make the plots under Monotonicity and Robustness.

Monotonicity

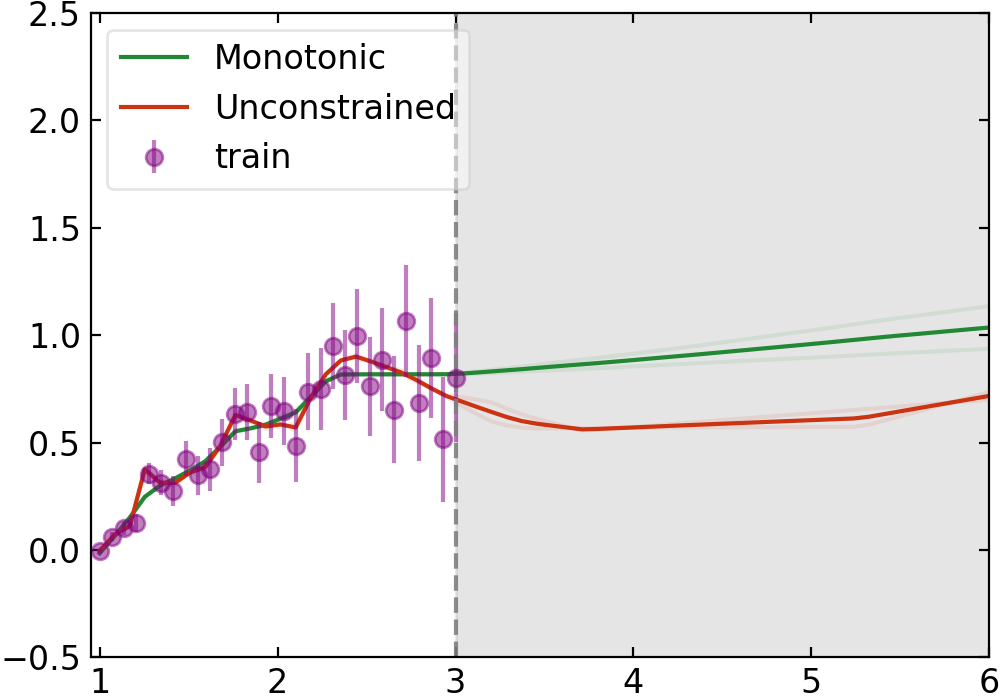
We will make a simple toy regression model to fit the following 1D function $$f(x) = log(x) + \epsilon(x)$$ where $\epsilon(x)$ is a Gaussian noise term whose variance is linearly increasing in x. In this toy model, we will assume that we have good reason to believe that the function we are trying to fit is monotonic (despite non-monotnic behavior of the noise). For example, we are building a trigger algorithm to discriminate between signal and background events. Rarer events are more likely to be signal and thus we should employ a network that is monotonic in some “rareness” feature. Another example could be a hiring classifier where (all else equal) higher school grades should imply better chances of being hired.

Training a monotonic NN and an unconstrained NN on the purple points and evaluating the networks on a uniform grid gives the following result:

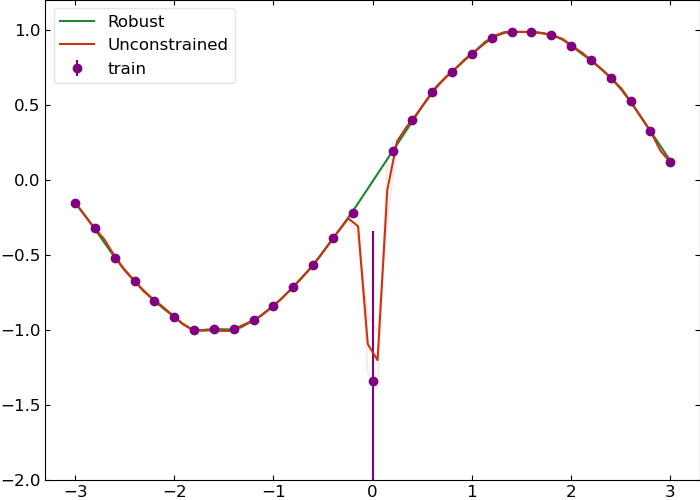
Robustness

Now we will make a different toy model with one noisy data point. This will show that the Lipschitz continuous network is more robust against outliers than an unconstrained network because its gradient with respect to the input is bounded between -1 and 1. Additionally, it is more robust against adversarial attacks/data corruption for the same reason.

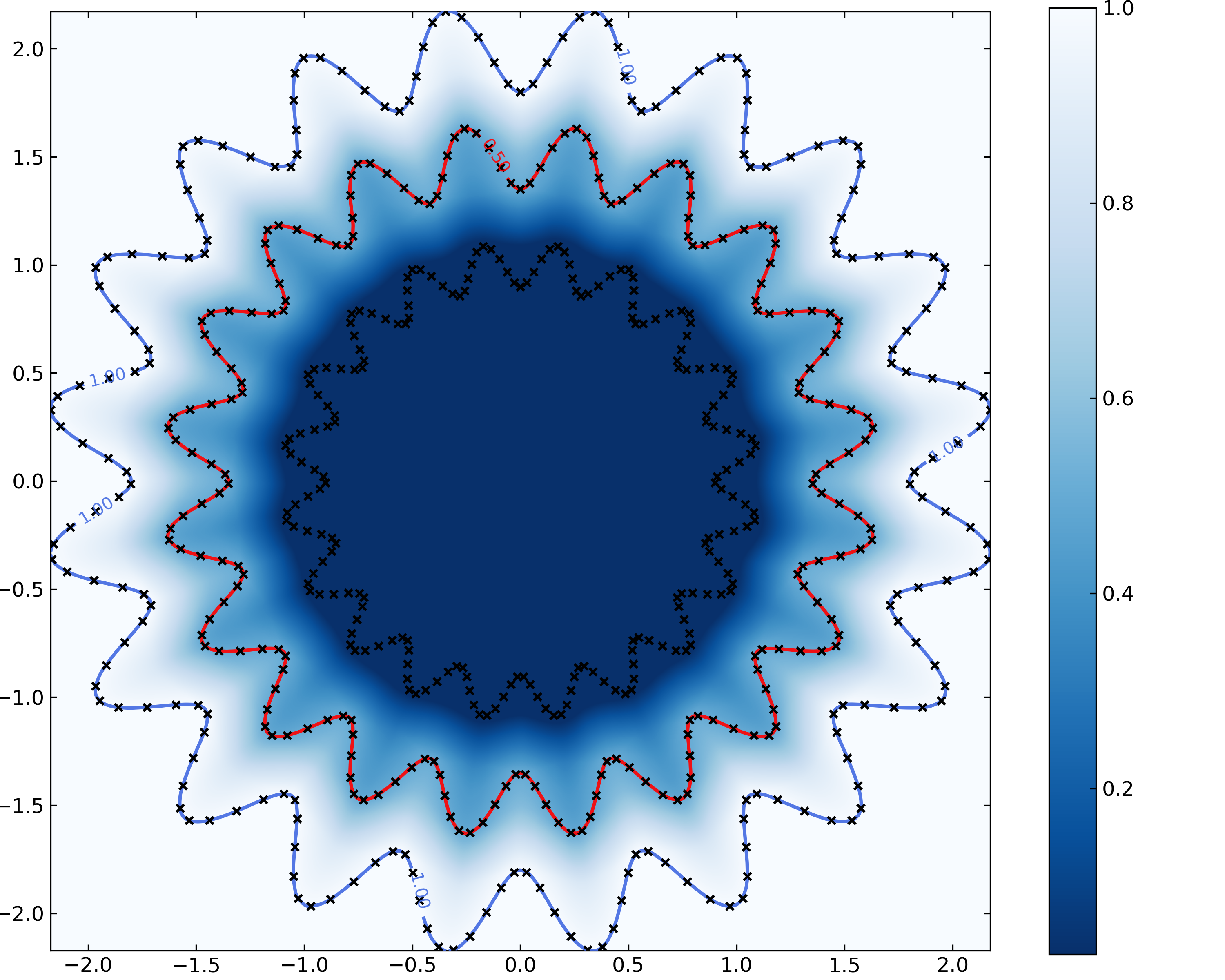
Lipschitz NNs can describe arbitrarily complex boundaries

GroupSort weight-constrained Neural Networks are universal approximators of Lipschitz continuous functions. Furthermore, they can describe arbitrarily complex decision boundaries in classification problems provided the proper objective function is used in training. In Examples\flower.py we provide code to regress on an example “complex” decision boundary in 2D.

Here are the contour lines of the resulting network (along with the training points in black).